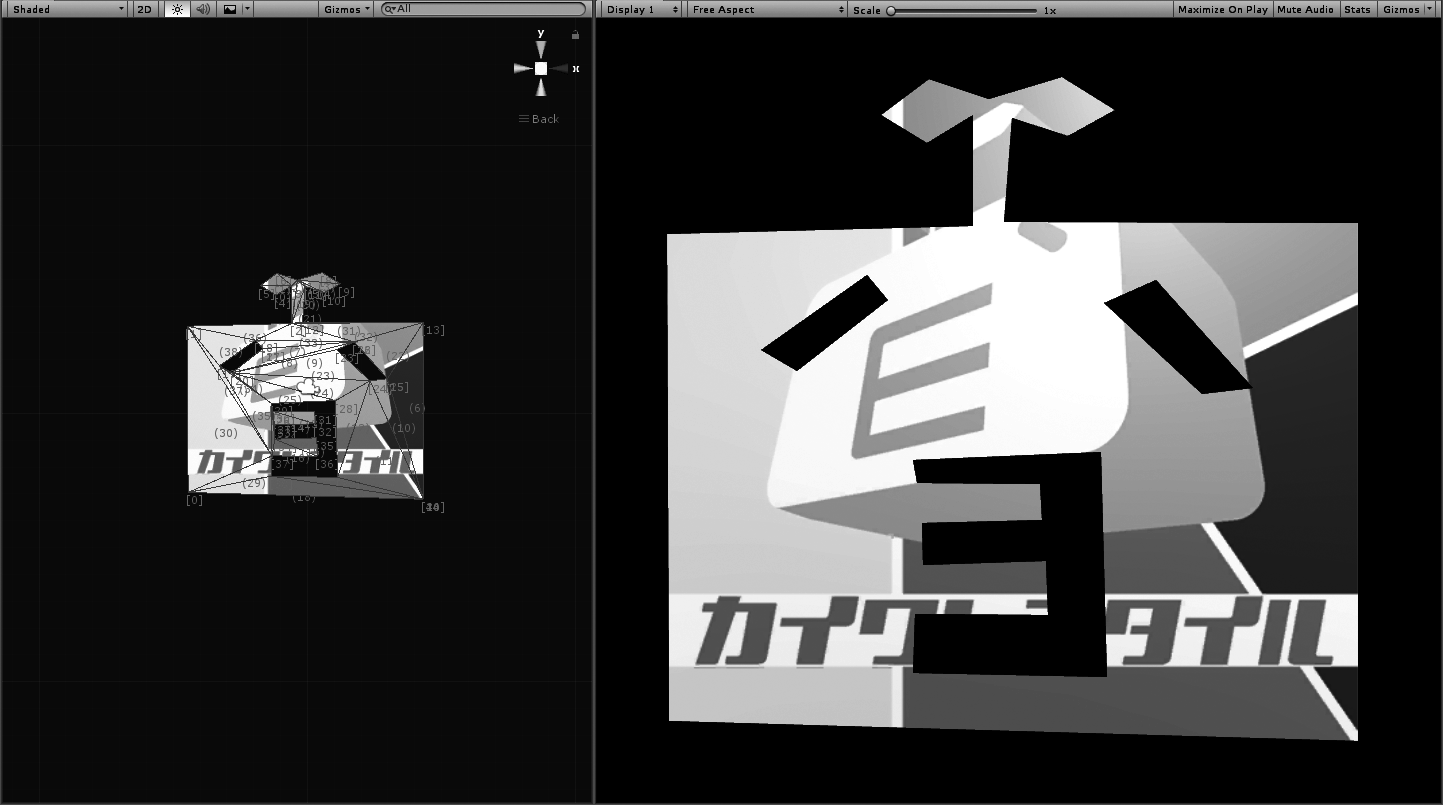
Figure 5.1: Screen of running the sample
In this chapter, we will explain one of the methods of dividing polygons into triangles, the "ear clipping method", hereinafter referred to as the "ear clipping method". In addition to the usual simple polygon triangulation, we will also explain the triangular division of polygons with holes and polygons that have a hierarchical structure.
The sample in this chapter is "TriangulationByEarClipping" from
https://github.com/IndieVisualLab/UnityGraphicsProgramming4
.
Run the sample DrawTest scene. Left-click on GameView to make a dot on the screen. Continue left-clicking on another point to connect it with the first point with a line. If you repeat it, you will get a polygon. When drawing lines, be careful not to cross the lines. Right-click to split the polygon into triangles to generate a mesh. If you generate a polygon in the generated mesh, you will get a polygon with holes.

Figure 5.1: Screen of running the sample
A simple polygon is a closed polygon that does not intersect at its own line segment.
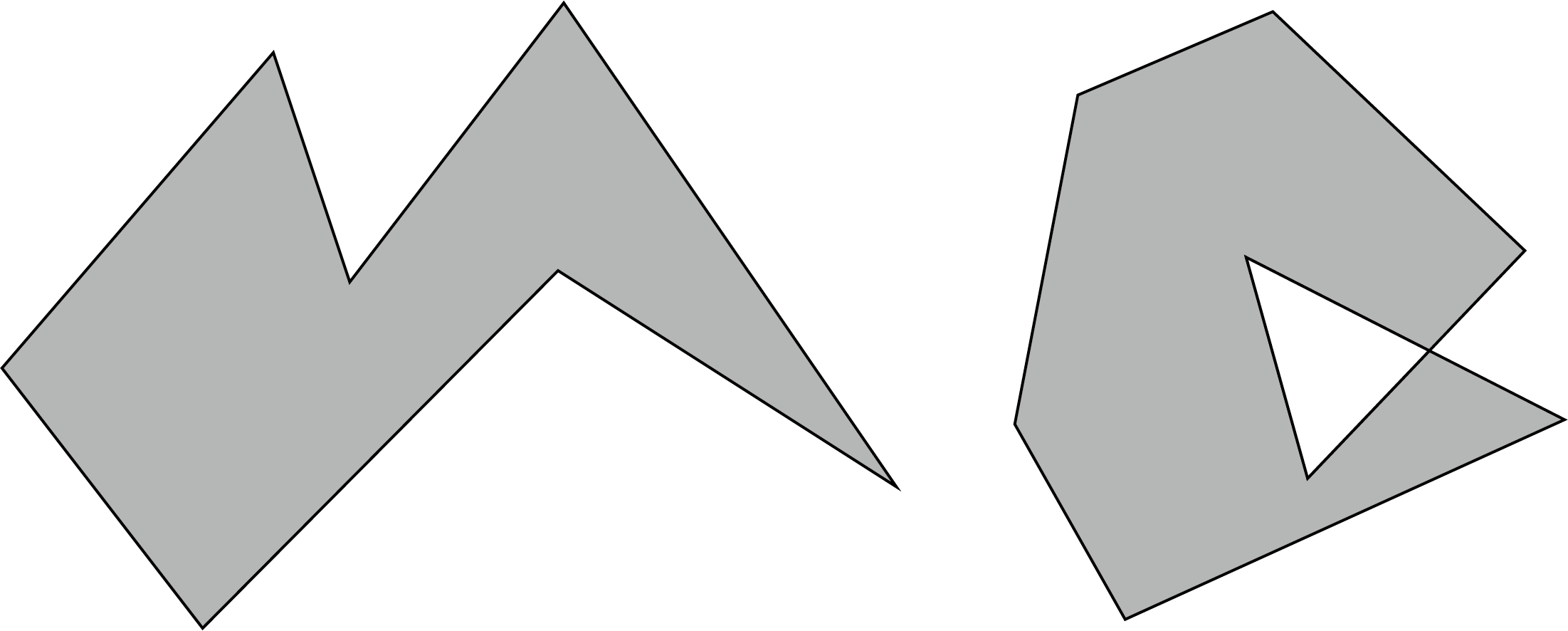
Figure 5.2: Left: Simple polygon, Right: Non-simple polygon
Any simple polygon can be triangulated. Dividing a simple polygon with n vertices into triangles creates n-2 triangles.
There are many methods for dividing polygons into triangles, but this time we will explain the "ear cutting method", which is simple to implement. The "ear-cutting method" is divided based on the theorem "Two ears the orem". This "Ear" refers to "a triangle whose two sides are polygonal sides and the remaining one side exists inside the polygon", and this theorem states that "four or more sides". A simple polygon without a hole with has at least two ears. "
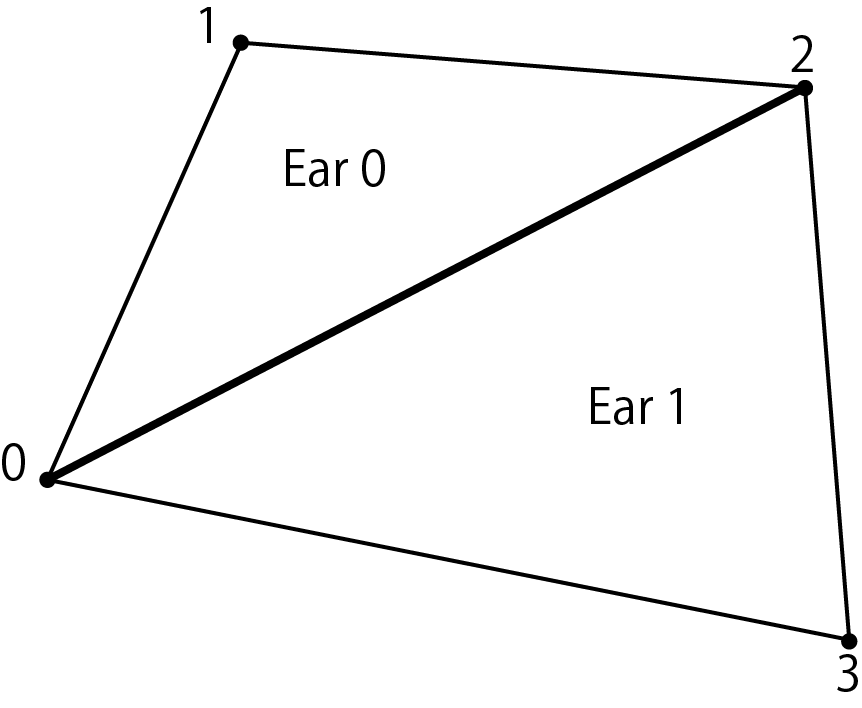
Figure 5.3: Ears
The "ear trimming method" is an algorithm that searches for this "ear" triangle and removes it from the polygon. This "ear cutting method" is simpler than other division algorithms, but it is slow, so I don't think it can be used very much in situations where speed is required.
First, look for "ears" in the given array of polygon vertices. The conditions for "ears" are the following two points.
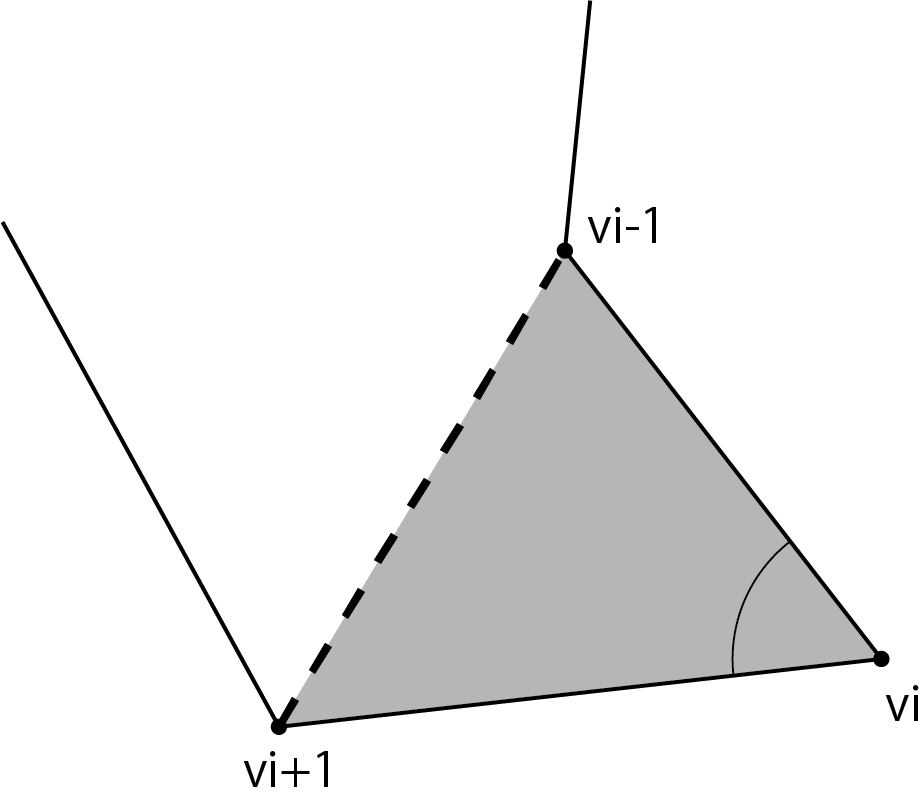
Figure 5.4: Ear conditions (within 180 degrees, no other vertices in the triangle)
Add the vertex vi that meets the above conditions to the ear list. This is done by the InitializeVertices function in the sample Triangulation.cs. Then create the triangles that make up the ear from the top of the ear list and remove the vertex vi from the vertex array.
Removing the vertex vi changes the shape of the polygon. For the remaining vertices vi-1, vi + 1, perform the above ear judgment again. If vertices vi-1, vi + 1 meet the ear criteria, they will be added to the end of the ear list, but they may also be removed from the ear list. This process corresponds to the CheckVertex function and EarClipping function of the sample Triangulation.cs.
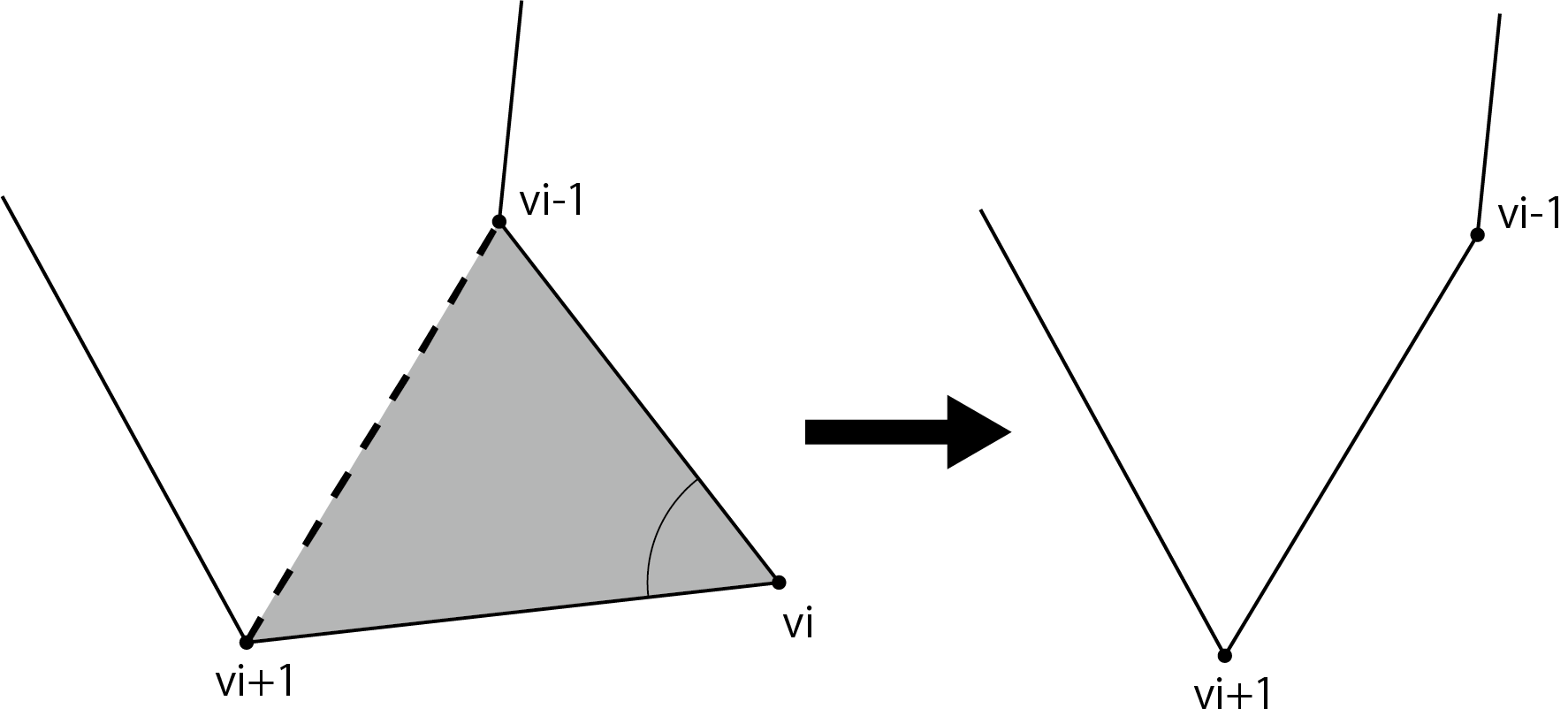
Figure 5.5: Polygon before and after deleting vertex vi
Let's illustrate a series of flows using a simple polygon as an example.
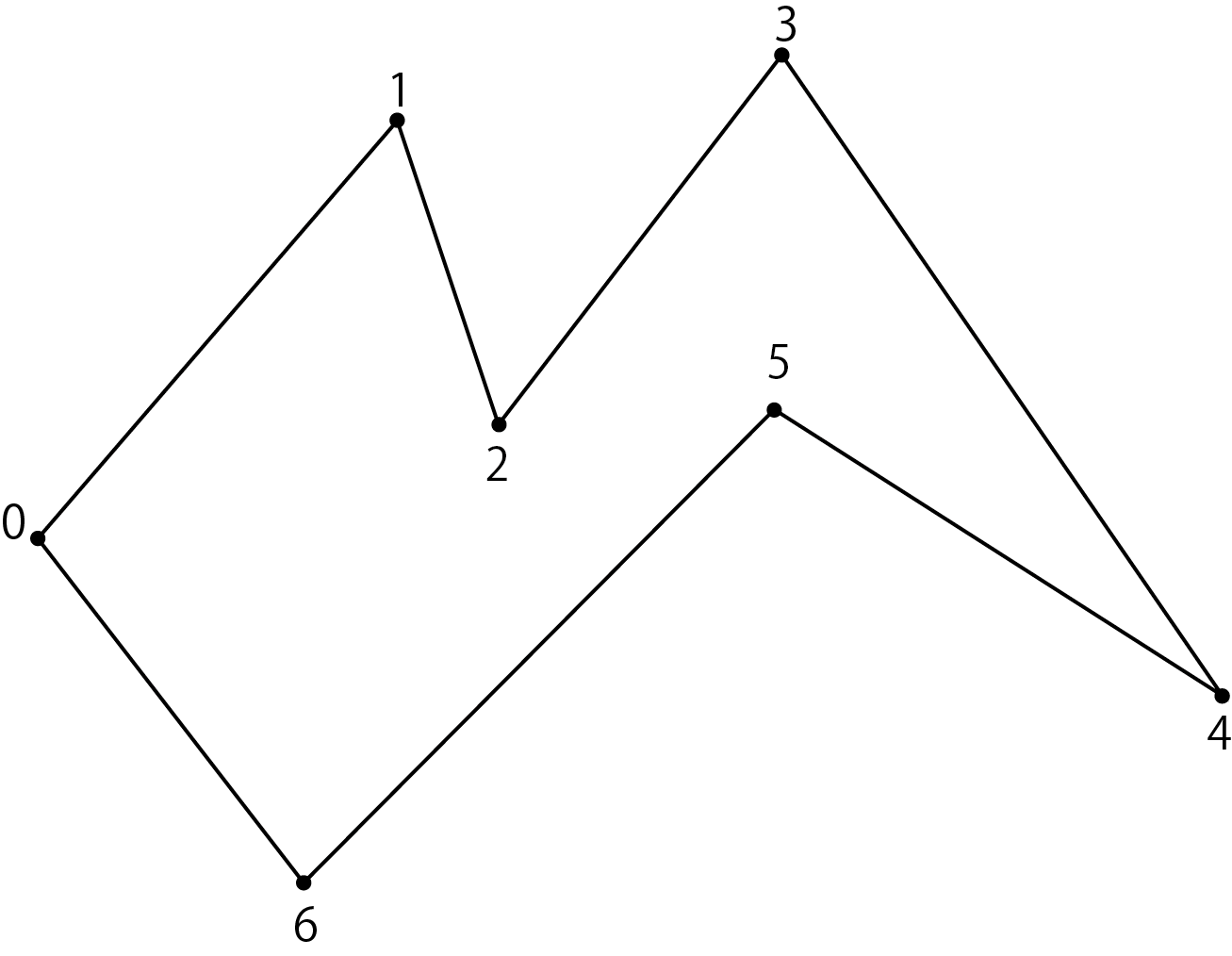
Figure 5.6: A simple polygon
First, look for your ears. In this case, the ear list contains vertices 0,1,4,6. Vertices 2 and 5 are excluded because they are not convex vertices, and vertices 3 are excluded because they are contained in triangles 2, 3 and 4.
First, take out the first vertex 0 of the ear list. Make a triangle with vertices 1 and 6 before and after vertex 0. Remove vertex 0 from the vertex array and connect the previous and next vertices 1 and 6 to form a new polygon. Then, the ears are judged for vertices 1 and 6. Originally both were ears, but they remain ears even after the ear judgment. The ear list at this time is 1,4,6.
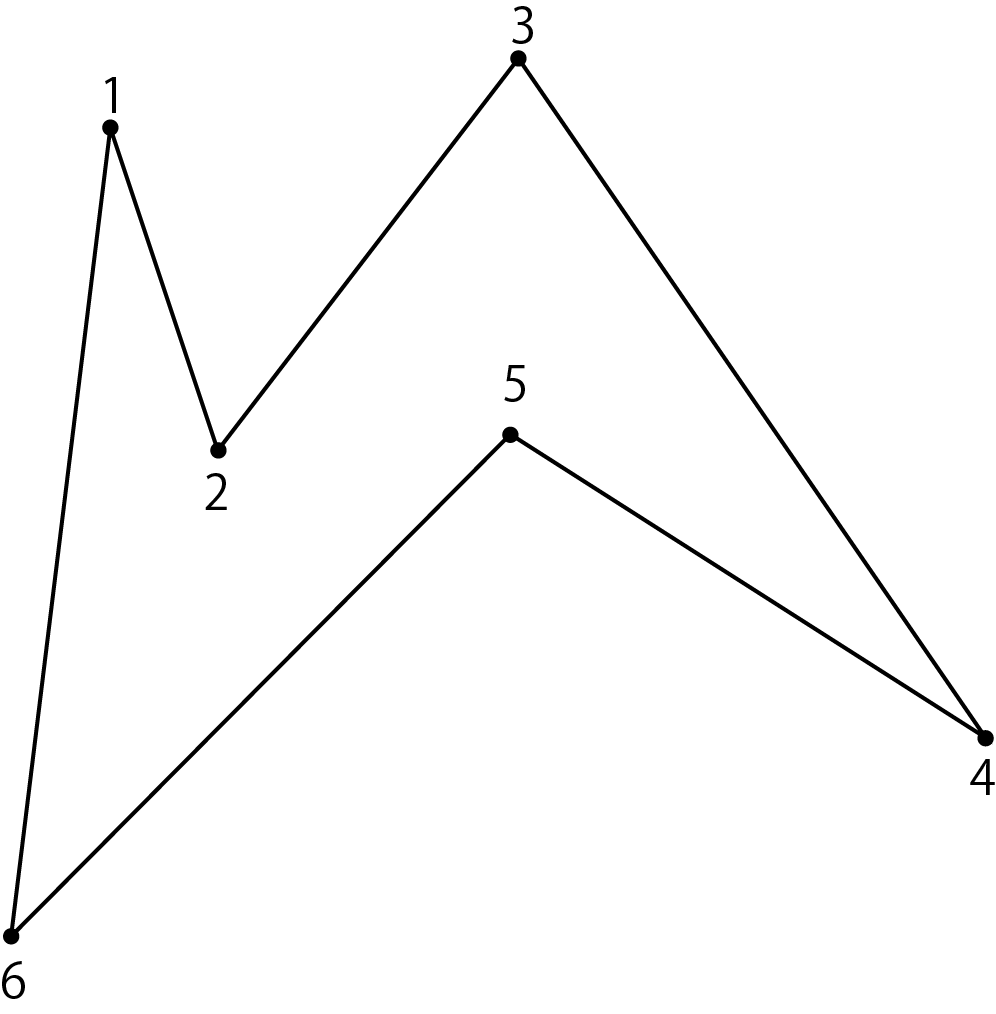
Figure 5.7: Polygon with 0 vertices removed
Then take vertex 1 from the beginning of the ear list. Make a triangle with vertices 2 and 6 before and after vertex 1. Remove vertex 1 from the vertex array and connect the previous and next vertices 2 and 6 to form a new polygon. Then, the ears are judged for vertices 2 and 6. Since the vertex 1 is gone, the vertex 2 becomes a convex vertex and the ear condition is satisfied, so add it to the ear list. Vertex 6 remains in the ear. The ear list at this time is 4,6,2.
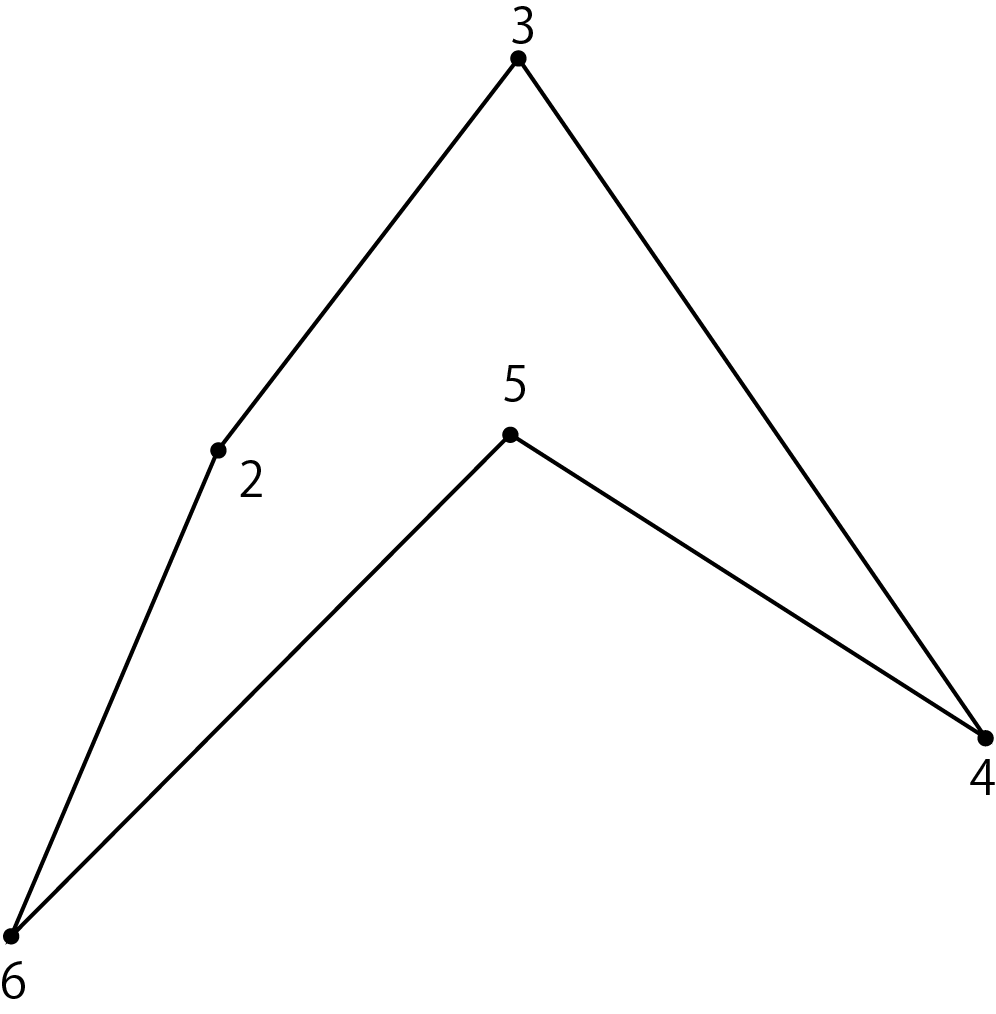
Figure 5.8: Polygon with vertex 1 removed
Then take vertex 4 from the top of the ear list. Make a triangle with vertices 3 and 5 before and after vertex 4. Remove vertex 4 from the vertex array and connect the previous and next vertices 3 and 5 to form a new polygon. Then, the ears are judged for vertices 3 and 5. With the disappearance of vertex 4, the triangle created by vertices 2 and 5 before and after vertex 3 no longer contains other vertices, so add vertex 3 to the ear list. Also, since the internal angle of vertex 5 is 180 degrees or less, it becomes a convex vertex and the ear condition is satisfied, so add it to the ear list. The ear list at this time is 6,2,3,5.
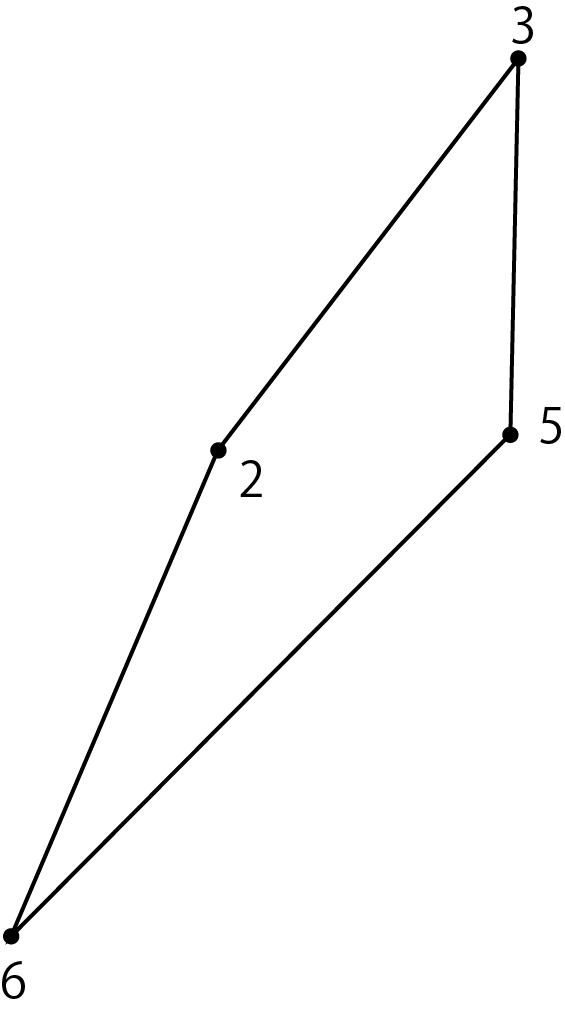
Figure 5.9: Polygon with vertex 4 removed
Then take vertex 6 from the top of the ear list. Make a triangle with vertices 2 and 5 before and after vertex 6. Remove vertex 6 from the vertex array and connect the previous and next vertices 2 and 5 to form a new polygon. Then, the ears are judged for vertices 2 and 5. Originally both were ears, but they remain ears even after the ear judgment. The ear list at this time is 2,3,5.
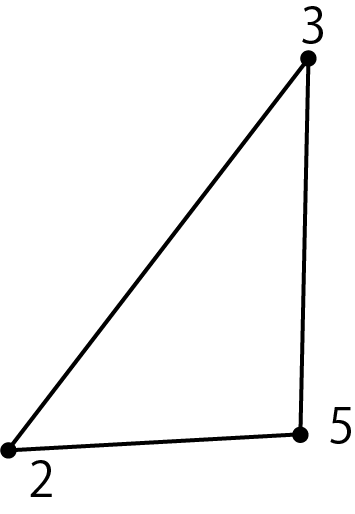
Figure 5.10: Polygon with vertex 6 removed
Next, I took out vertex 2 from the top of the ear list ... I thought, but since there are only 3 vertices of the polygon left, I made a triangle as it is and the triangle division is finished. The final result of the triangle split is:
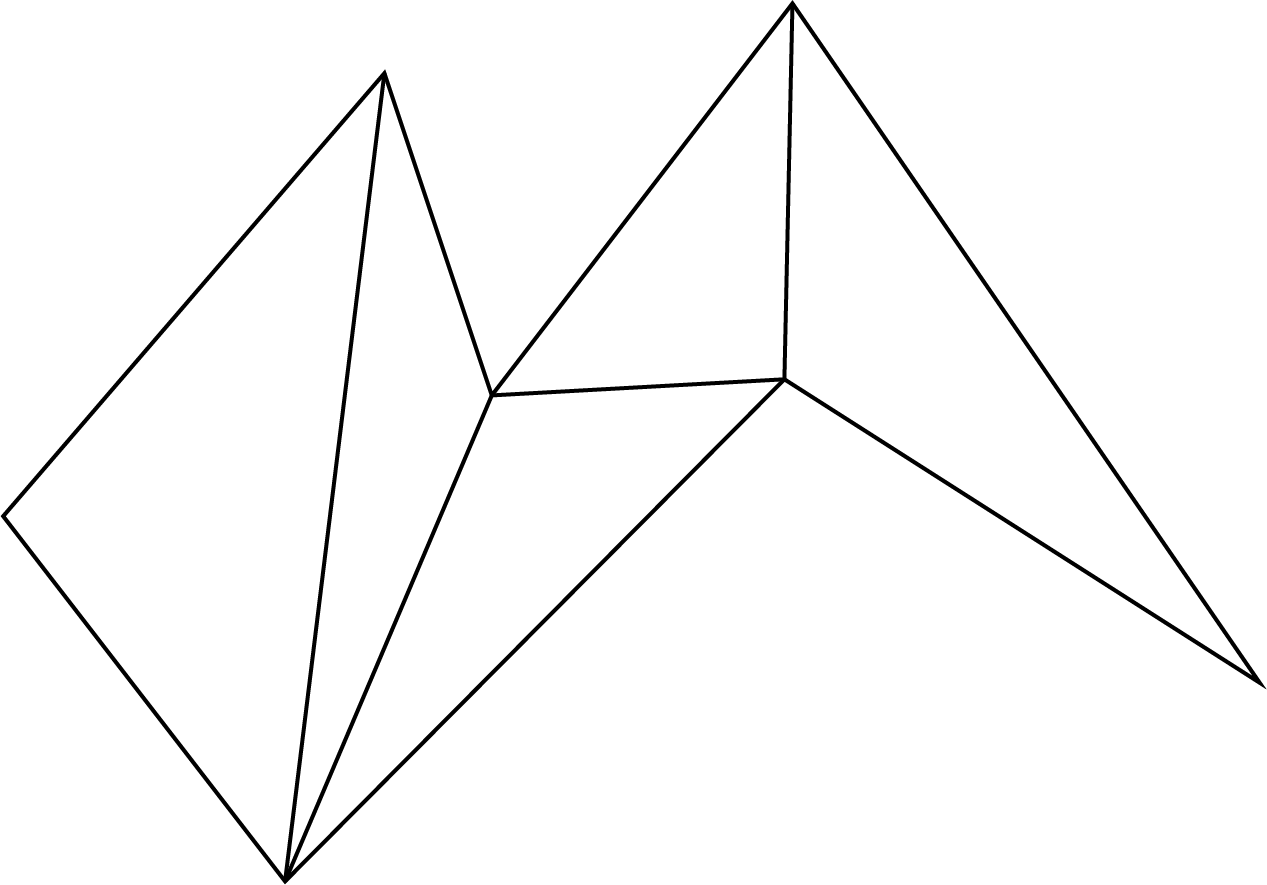
Figure 5.11: Triangular division result
Next, I will explain the triangular division of a polygon with holes. Originally, the "ear cutting method" cannot be applied to polygons with holes, but if you make a notch in the outer polygon and connect it to the inner polygon as shown in the figure, the inner polygon will be the outer polygon. It will be part of the and you will be able to apply the ear-cutting method. This method is also possible for polygons with multiple holes.
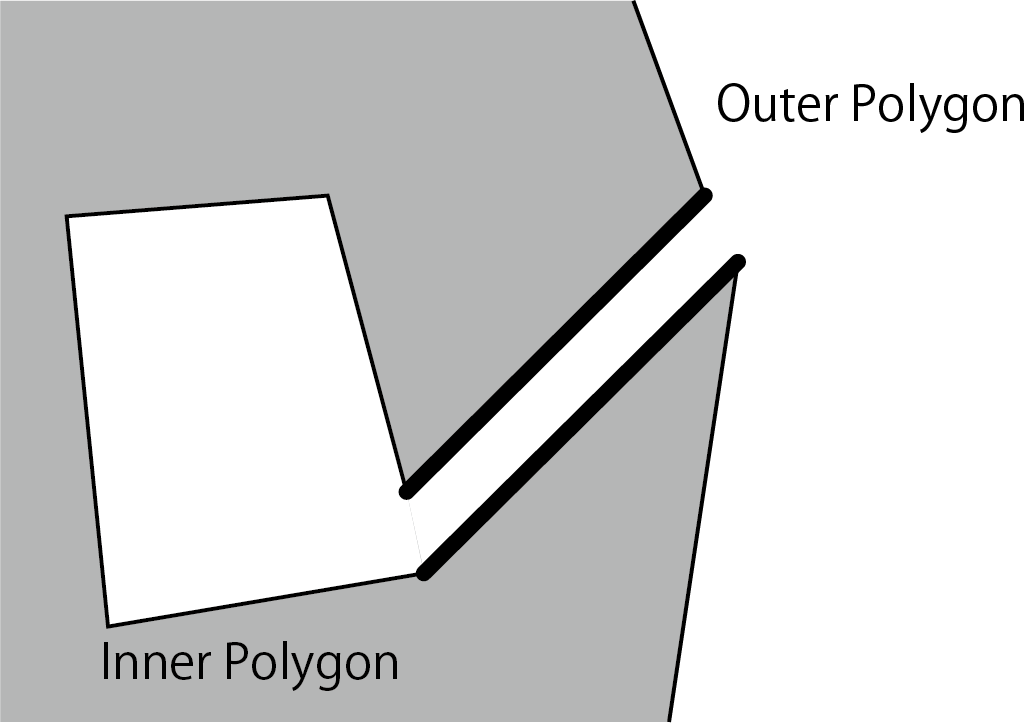
Figure 5.12: Joining inner and outer polygons (figure is a fairly exaggerated representation)
As a premise, the order of the vertices of the outer and inner polygons must be reversed. For example, if the outer polygon has vertices aligned clockwise, the inner polygon must align counterclockwise. The flow of joining is explained using the following polygon as an example.
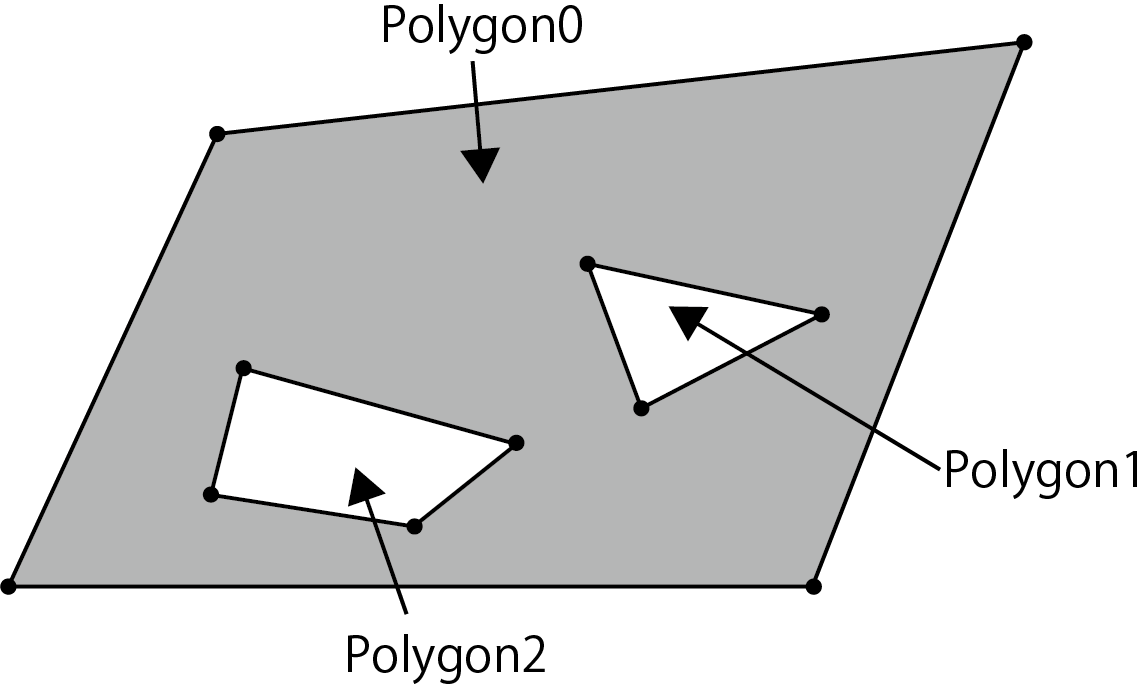
Figure 5.13: Polygon with holes
1. If there are multiple holes (inner polygons), look for the polygon with the largest X coordinate (on the right) and its vertices among the inner polygons.
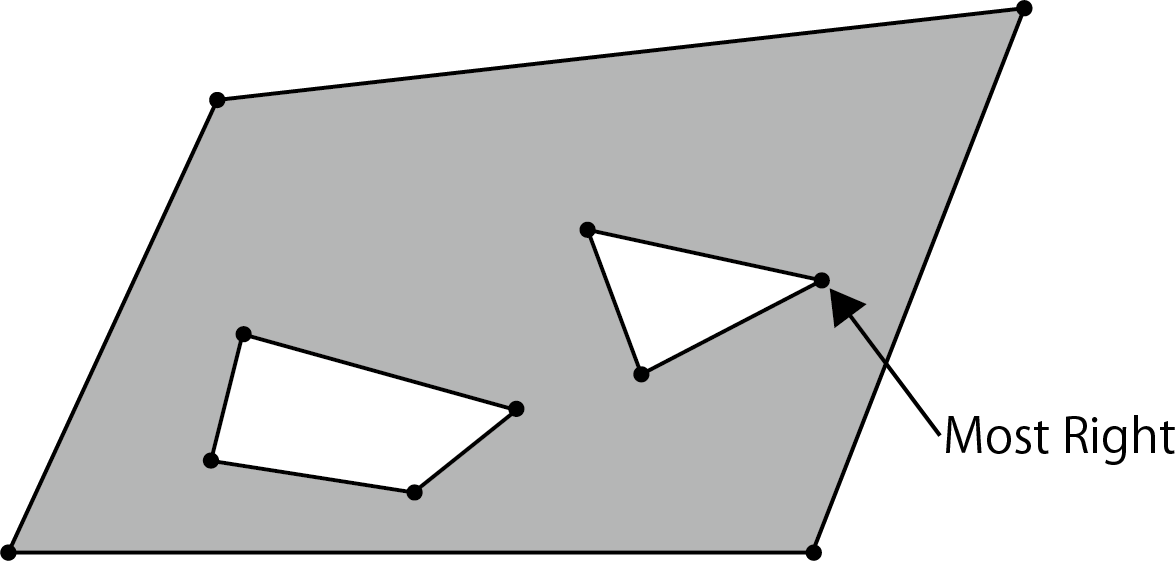
Figure 5.14: Vertex with the highest X coordinate
2. Let M be the vertex with the largest X coordinate. Draw a straight line from M to the right.
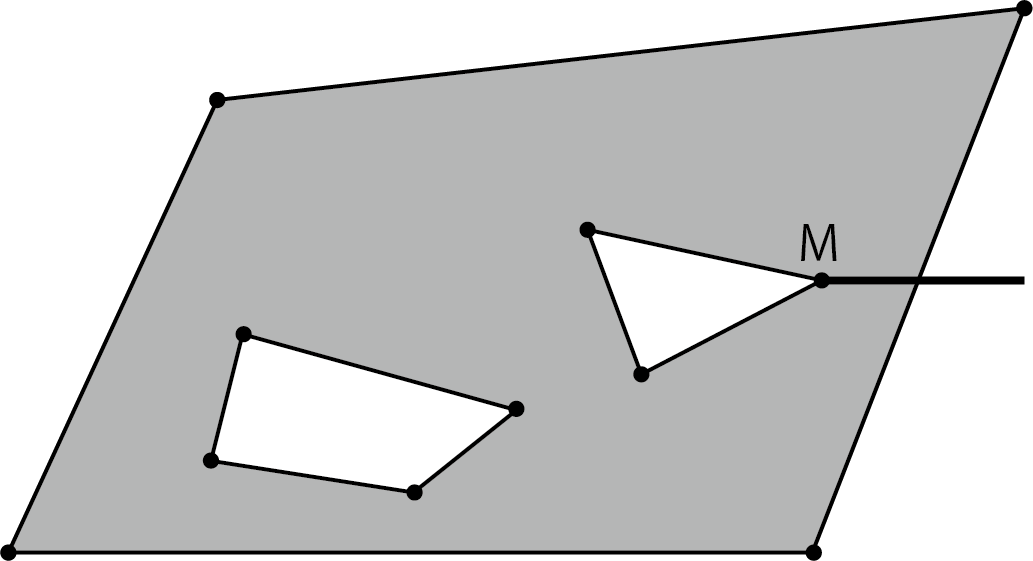
Figure 5.15: Draw a line to the right from vertex M
3. Find the edge and intersection I of the outer polygon that intersects the line extending to the right from vertex M. If it intersects multiple sides, select the side of the intersection closest to vertex M.
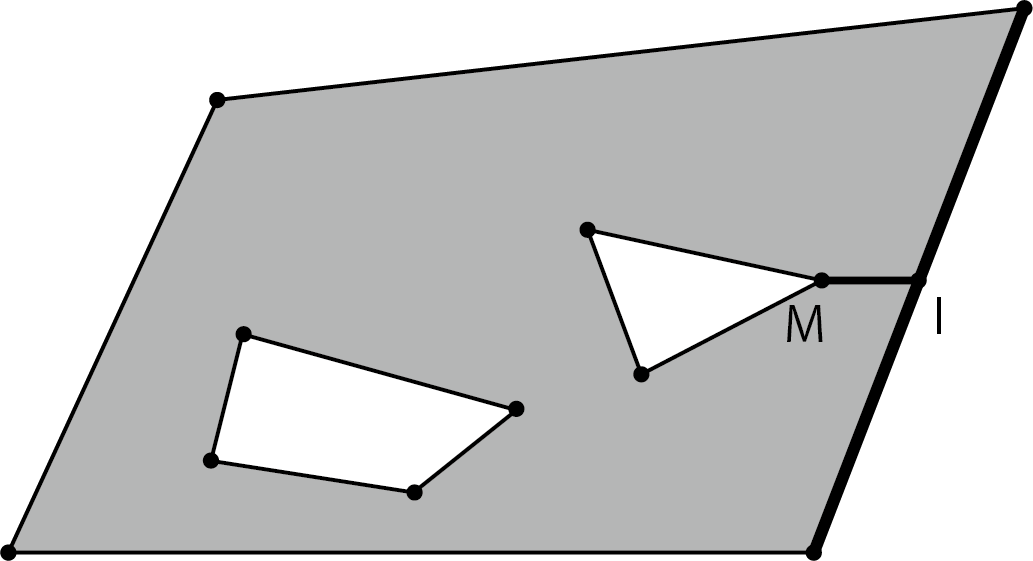
Figure 5.16: Vertex M and intersection I
4. Select the vertex P with the largest X coordinate among the vertices of the intersecting sides. Check if the triangle connecting the vertices M, I, P contains other vertices.
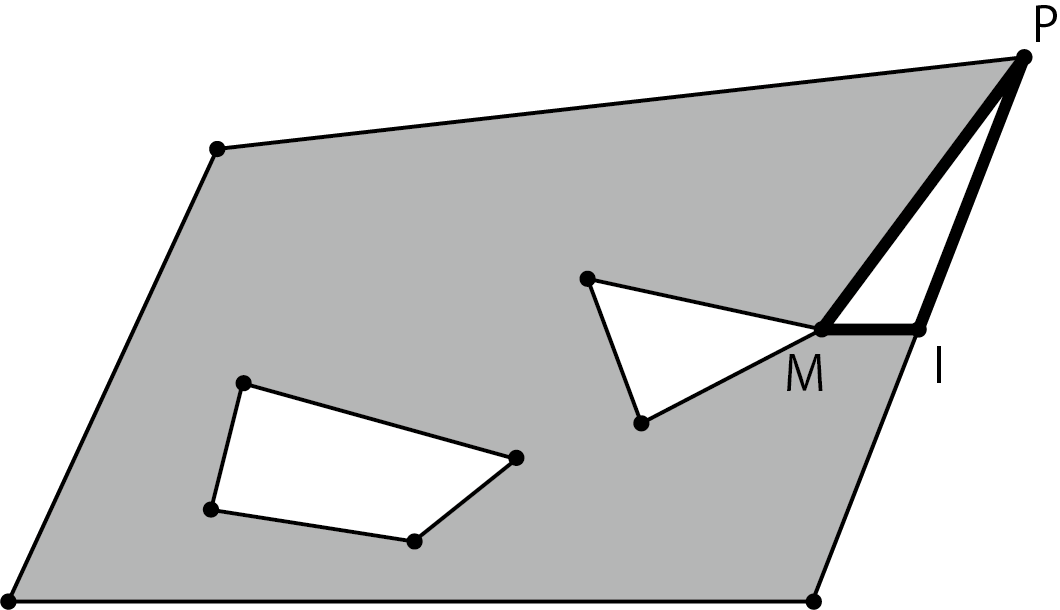
Figure 5.17: Triangle M, I, P
5. If the triangles M, I, P do not contain other vertices, it can be divided, so connect the vertices P of the outer polygon to the vertices M of the inner polygon, and turn the inner polygon counterclockwise. I will go around. When connecting from M to the vertex P of the outer polygon again, the vertex M and the vertex P are duplicated to make another vertex (vertex M', P'). By separating the incoming line and the outgoing line, the lines seem to overlap, but the order of the vertices is a simple polygon that does not intersect.
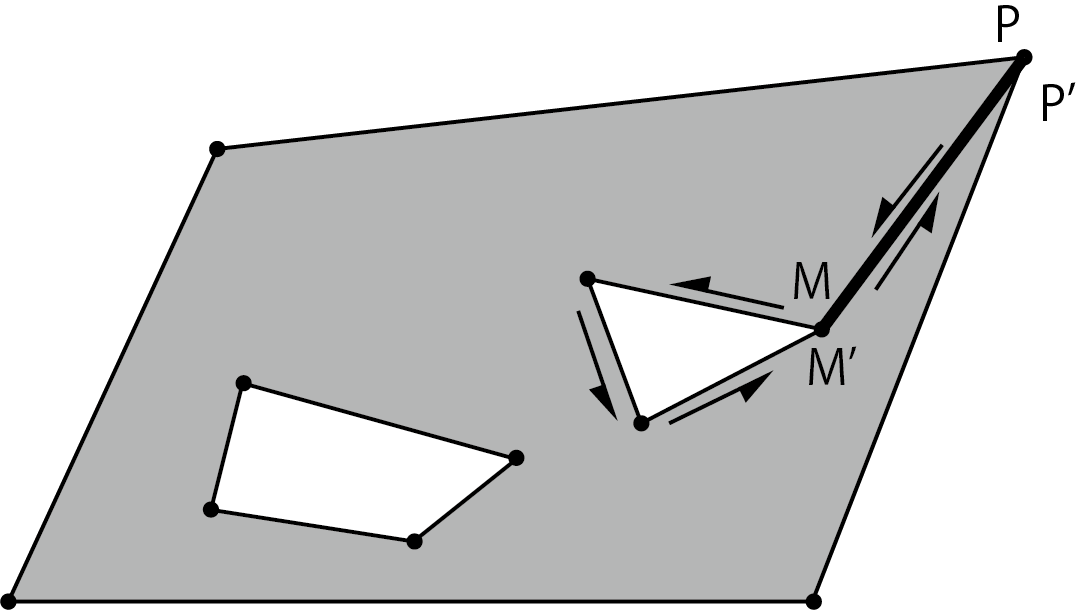
Figure 5.18: A diagram connecting the outer polygon and the inner polygon
6. If the triangles M, I, P contain other vertices R, select that vertex R, but if multiple vertices are included, line segments M, I and line segment M Select the vertex R with the smallest angle θ formed by, R, and perform processing 5.
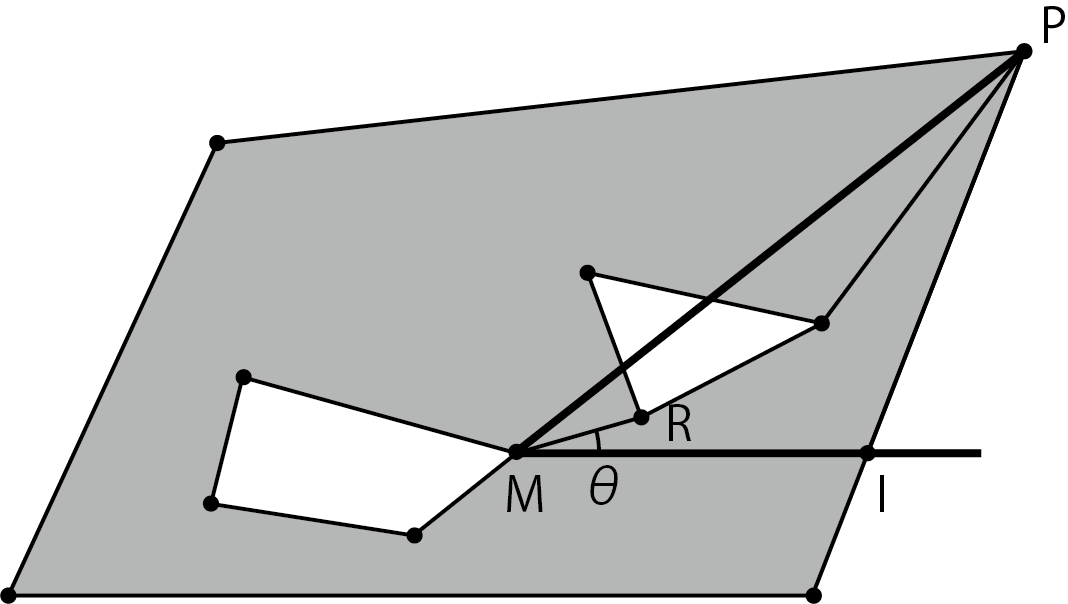
Figure 5.19: Vertex R with the smallest angle θ formed by line segments MI and MR
7. Go back to 1 and join with the other inner polygons.
Next, I will explain the triangular division of a nested polygon. Since the process of joining polygons with holes and the process of dividing triangles were explained in the previous section, here we will mainly explain the procedure for building a tree of parent-child relationships of polygons.
Let's take the following set of polygons as an example.
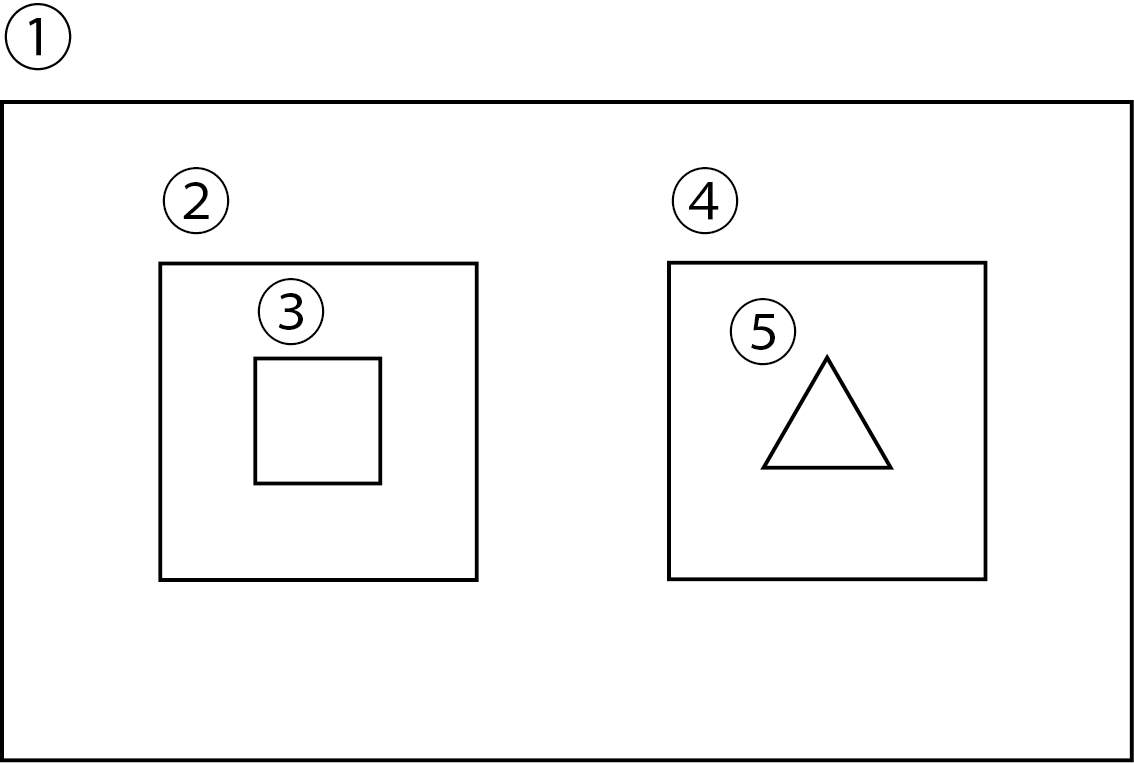
Figure 5.20: Nested polygons
When you create a polygonal parent-child relationship, you get the following tree.
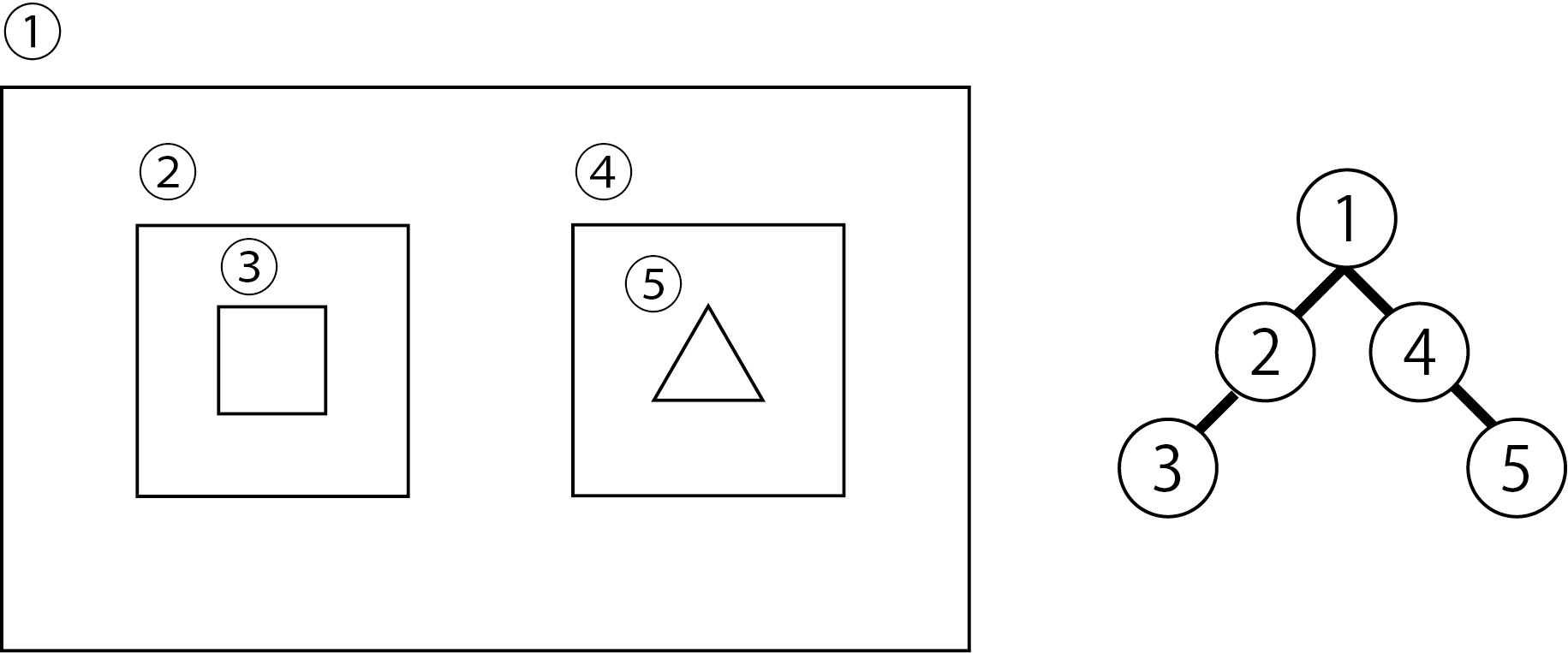
Figure 5.21: Left: Nested polygon Right: Parent-child relationship
Extract polygon 1 at the top of the tree (excluding dummies) and polygons 2 and 4 of its children.
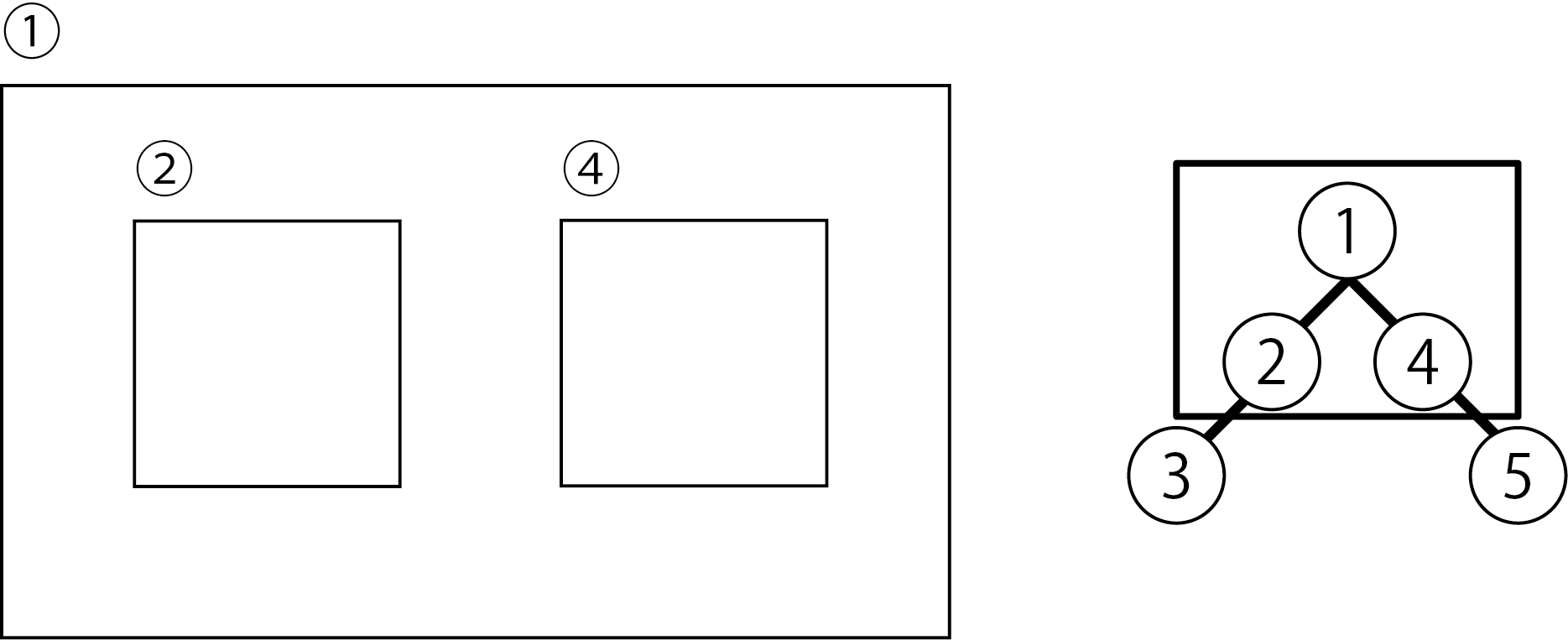
Figure 5.22: Extract polygons 1, 2 and 4
Join polygons 1, 2 and 4 in order from the right.
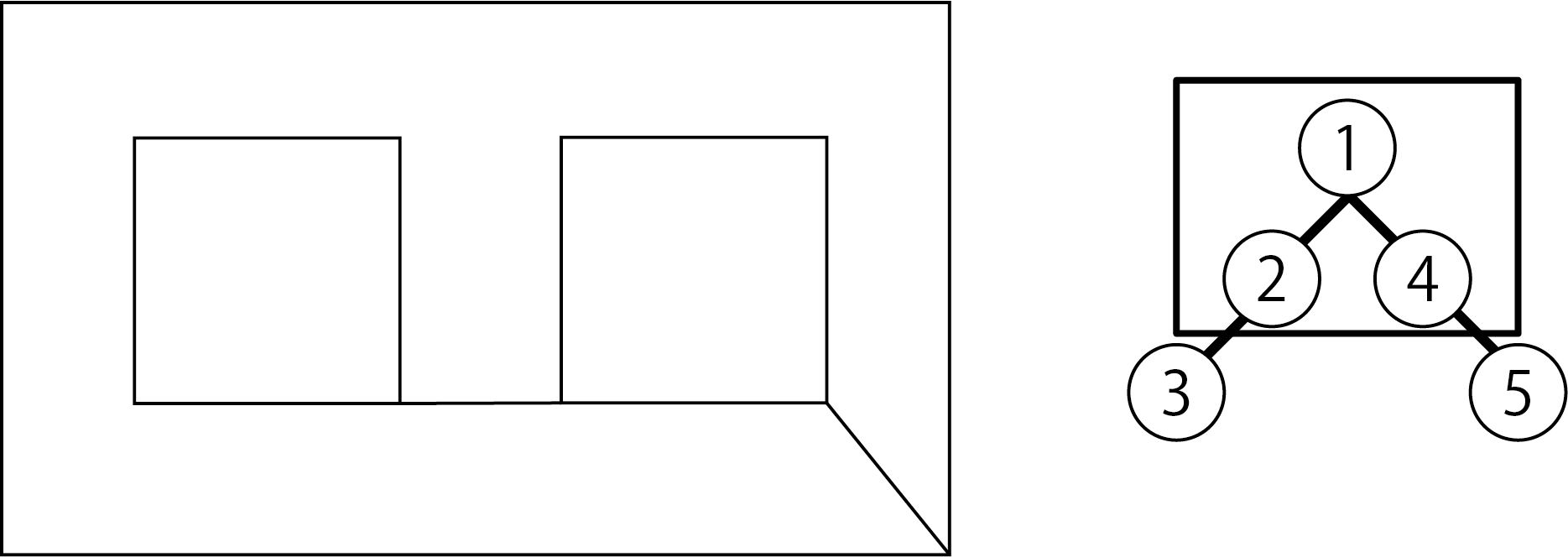
Figure 5.23: Joining polygons 1, 2 and 4
Divide the combined polygon into triangles.
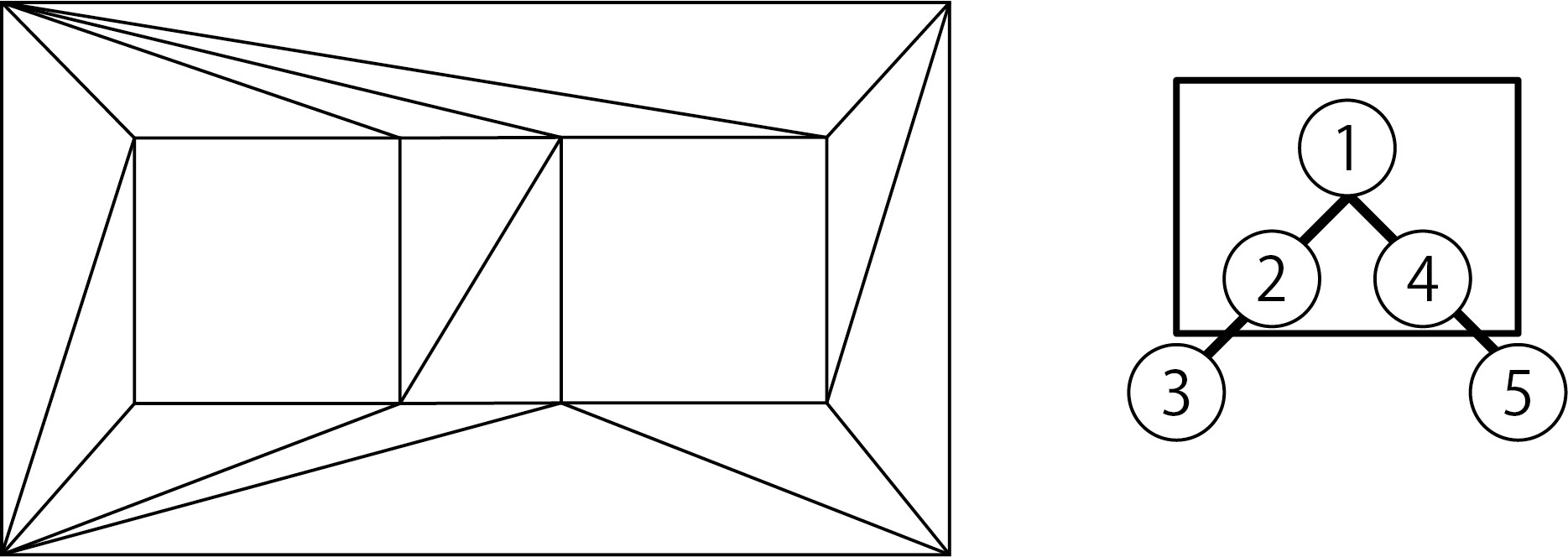
Figure 5.24: Triangulation of combined polygons
Remove the polygon that is divided into triangles. The rest of the parent-child relationship tree is 3 and 5. First, take it out from 3.

Figure 5.25: Polygon 3
Since 3 has no children, it is divided into triangles as it is.

Figure 5.26: Polygon 3 divided into triangles
Remove the polygon that is divided into triangles. There are only 5 left in the parent-child relationship tree. 5 is a triangle and has no children, so it ends as it is. This completes the triangular division of the nested polygon.

Figure 5.27: Last polygon 5
Let's move on to the explanation of the sample source code that implements all three algorithms explained so far.
First, define a Polygon class that manages an array of polygon vertices. The Polygon class holds information such as the array of vertex coordinates and the direction of the loop, and determines whether a polygon is included in the polygon.
Polygon.cs
public class Polygon
{
// Loop direction
public enum LoopType
{
CW, // clockwise
CCW, // counterclockwise
ERR, // Indefinite (no orientation)
}
public Vector3 [] vertices; // Vertex array
public LoopType loopType; // Loop direction
// ~ omitted ~
}
This is a Triangulation class that actually divides a polygon into triangles. The main is the Triangulate function of the Triangulation class.
Data structure definition in Triangulation.cs
// Vertex array List<Vector3> vertices = new List<Vector3>(); // List of vertex numbers (let's end and start connected) LinkedList<int> indices = new LinkedList<int>(); // Ear vertex list List<int> earTipList = new List<int>();
It defines vertices that stores the array of vertex coordinates of the polygon to be processed, indices that stores the number (index) of the vertices of the polygon, and earTipList that stores the ears. Since indices need to refer to the vertices before and after, we use LinkedList, which has the property of a bidirectional list.
First, if you are given an array of vertices that make up a polygon from the outside, store it in the list as a Polygon class.
Polygon list
// Polygon list
List<Polygon> polygonList = new List<Polygon>();
public void AddPolygon(Polygon polygon)
{
polygonList.Add(polygon);
}
At the beginning of the Triangulate function, sort the Polygon list with polygonal data added in descending order of area of the rectangular area.
Sorted part of Polygon list
// Sort in descending order of area of rectangular area in polygon list polygonList.Sort((a, b) => Mathf.FloorToInt( (b.rect.width * b.rect.height) - (a.rect.width * a.rect.height) ));
Next, we will pack the sorted Polygon list into the TreeNode class that creates the tree structure.
The part that packs the Polygon list into a TreeNode
// Create route (empty)
polygonTree = new TreeNode<Polygon>();
// Create a polygonal hierarchy
foreach (Polygon polygon in polygonList)
{
TreeNode<Polygon> tree = polygonTree;
CheckInPolygonTree(tree, polygon, 1);
}
The TreeNode looks like this: I think it's a common tree structure, but for an empty top-level node, it defines a flag isValue for the existence of its contents.
TreeNode.cs
public class TreeNode<T>
{
public TreeNode<T> parent = null;
public List<TreeNode<T>> children = new List<TreeNode<T>>();
public T Value;
public bool isValue = false;
public TreeNode(T val)
{
Value = val;
isValue = true;
}
public TreeNode()
{
isValue = false;
}
public void AddChild(T val)
{
AddChild(new TreeNode<T>(val));
}
public void AddChild(TreeNode<T> tree)
{
children.Add(tree);
tree.parent = this;
}
public void RemoveChild(TreeNode<T> tree)
{
if (children.Contains(tree))
{
children.Remove(tree);
tree.parent = null;
}
}
}
Returning to Triangulation.cs, it is the contents of the CheckInPolygonTree function that creates a hierarchical structure of polygons. It checks whether the passed polygon fits inside its own polygon, and recursively determines whether it fits inside its own children. Makes the passed polygon its own child if it is included in itself but not in its children, or if there are no children.
CheckInPolygonTree関数
bool CheckInPolygonTree(TreeNode<Polygon> tree, Polygon polygon, int lv)
{
// Does it have a polygon?
bool isInChild = false;
if (tree.isValue)
{
if (tree.Value.IsPointInPolygon(polygon))
{
// If it is included in itself, search if it is also included in the child
for(int i = 0; i < tree.children.Count; i++)
{
isInChild |= CheckInPolygonTree(
tree.children[i], polygon, lv + 1);
}
// Make it your own child if it is not included in the child
if (!isInChild)
{
// Invert the order of the vertices if necessary
// CW because it is Inner when even nesting
// CCW because it is Outer when odd nesting
if (
((lv % 2 == 0) &&
(polygon.loopType == Polygon.LoopType.CW)) ||
((lv % 2 == 1) &&
(polygon.loopType == Polygon.LoopType.CCW))
)
{
polygon.ReverseIndices();
}
tree.children.Add(new TreeNode<Polygon>(polygon));
return true;
}
}
else
{
// not included
return false;
}
}
else
{
// Search only for children if they have no value
for (int i = 0; i < tree.children.Count; i++)
{
isInChild |= CheckInPolygonTree(
tree.children[i], polygon, lv + 1);
}
// Make it your own child if it is not included in the child
if (!isInChild)
{
// Invert the order of the vertices if necessary
// CW because it is Inner when even nesting
// CCW because it is Outer when odd nesting
if (
((lv % 2 == 0) &&
(polygon.loopType == Polygon.LoopType.CW)) ||
((lv % 2 == 1) &&
(polygon.loopType == Polygon.LoopType.CCW))
)
{
polygon.ReverseIndices();
}
tree.children.Add(new TreeNode<Polygon>(polygon));
return true;
}
}
return isInChild;
}
If there are multiple inner polygons, select the vertex with the largest X coordinate among the inner polygons and that polygon. At that time, define a class that collects the X coordinate, vertex number, and polygon number information for judgment.
XMaxData structure
/// <summary>
/// X coordinate maximum value and polygon information
/// </summary>
struct XMaxData
{
public float xmax; // x coordinate maximum value
public int no; // Polygon number
public int index; // vertex number of xmax
public XMaxData(float x, int n, int ind)
{
xmax = x;
no = n;
index = ind;
}
}
Next, the actual joining process is divided into two processes: sorting multiple polygons in descending order of X coordinate, and joining. The first is the process of sorting multiple polygons in descending order of X coordinate.
CombineOuterAndInners関数
Vector3[] CombineOuterAndInners(Vector3[] outer, List<Polygon> inners)
{
List<XMaxData> pairs = new List<XMaxData>();
// Find the inner polygon with the vertex with the largest X coordinate
for (int i = 0; i < inners.Count; i++)
{
float xmax = inners[i].vertices[0].x;
int len = inners[i].vertices.Length;
int xmaxIndex = 0;
for (int j = 1; j < len; j++)
{
float x = inners[i].vertices[j].x;
if(x > xmax)
{
xmax = x;
xmaxIndex = j;
}
}
pairs.Add(new XMaxData(xmax, i, xmaxIndex));
}
// Sort to the right (in descending order of xmax)
pairs.Sort((a, b) => Mathf.FloorToInt(b.xmax - a.xmax));
// Combine from right
for (int i = 0; i < pairs.Count; i++)
{
outer = CombinePolygon(outer, inners[pairs[i].no], pairs[i].index);
}
return outer;
}
Next is the join processing part. In the CombinePolygon function, draw a horizontal line from the vertex M with the largest X coordinate of the inner polygon and find the line segment of the outer polygon that intersects that line.
Early stage of CombinePolygon function
Vector3[] CombinePolygon(Vector3[] outer, Polygon inner, int xmaxIndex)
{
Vector3 M = inner.vertices[xmaxIndex];
// Find the intersection
Vector3 intersectionPoint = Vector3.zero;
int index0 = 0;
int index1 = 0;
if (GeomUtil.GetIntersectionPoint(M,
new Vector3(maxX + 0.1f, M.y, M.z),
outer, ref intersectionPoint,
ref index0, ref index1))
{
~ Omitted ~
GeometryUtil.GetIntersectionPoint, a function that finds the intersection of line segments M and I and the line segment of the outer polygon, is as follows. The point is that the outer polygon is clockwise, so we only look for those whose starting point is above the line segments M and I and whose end point is below. Doing so will prevent the vertices from getting out of order if you select a line segment that connects the outer polygon to the inner polygon in the already joined inner and outer polygons.
GetIntersectionPoint function
public static bool GetIntersectionPoint(Vector3 start, Vector3 end,
Vector3[] vertices,
ref Vector3 intersectionP,
ref int index0, ref int index1)
{
float distanceMin = float.MaxValue;
bool isHit = false;
for(int i = 0; i < vertices.Length; i++)
{
int index = i;
int next = (i + 1)% vertices.Length; // Next vertex
Vector3 iP = Vector3.zero;
Vector3 vstart = vertices[index];
Vector3 vend = vertices[next];
// The starting point of the intersecting polygonal line segment must be at least the line segment M, I
Vector3 diff0 = vstart - start;
if (diff0.y < 0f)
{
continue;
}
// The end point of the intersecting polygonal line segment is below the line segment M, I
Vector3 diff1 = vend - start;
if (diff1.y > 0f)
{
continue;
}
if (IsIntersectLine(start, end, vstart, vend, ref iP))
{
float distance = Vector3.Distance(start, iP);
if (distanceMin >= distance)
{
distanceMin = distance;
index0 = index;
index1 = next;
intersectionP = iP;
isHit = true;
}
}
}
return isHit;
}
After finding the intersection, check if the triangle created from the vertex with the largest X coordinate of the intersecting line segment, vertex M, and intersection I contains other vertices. To determine if a triangle contains vertices, a two-dimensional cross product is used to determine which side of the triangle's line segment the vertices are on. If the vertices are to the right of all lines, they are inside the triangle.
IsTriangle and CheckLine functions in GeometryUtil.cs
/// <summary>
/// Returns the positional relationship between the line and the vertex
/// </summary>
/// <param name="o"></param>
/// <param name="p1"></param>
/// <param name="p2"></param>
/// <returns> +1: Right of line -1: Left of line 0: On line </ returns>
public static int CheckLine(Vector3 o, Vector3 p1, Vector3 p2)
{
double x0 = o.x - p1.x;
double y0 = o.y - p1.y;
double x1 = p2.x - p1.x;
double y1 = p2.y - p1.y;
double x0y1 = x0 * y1;
double x1y0 = x1 * y0;
double det = x0y1 - x1y0;
return (it> 0D? +1: (it <0D? -1: 0));
}
/// <summary>
/// Triangle (clockwise) and point inside / outside judgment
/// </summary>
/// <param name="o"></param>
/// <param name="p1"></param>
/// <param name="p2"></param>
/// <param name="p3"></param>
/// <returns> +1: outside -1: inside 0: online</returns>
public static int IsInTriangle(Vector3 o,
Vector3 p1,
Vector3 p2,
Vector3 p3)
{
int sign1 = CheckLine(o, p2, p3);
if (sign1 < 0)
{
return +1;
}
int sign2 = CheckLine(o, p3, p1);
if (sign2 < 0)
{
return +1;
}
int sign3 = CheckLine(o, p1, p2);
if (sign3 < 0)
{
return +1;
}
return (((sign1 != 0) && (sign2 != 0) && (sign3 != 0)) ? -1 : 0);
}
Now, the continuation of Combine Polygon. After finding the intersection, it is judged whether there are other vertices in the triangle, but the direction of the connection of the triangle is clockwise because the inside and outside judgment is made using the outer product.
Middle 1 of CombinePolygon function
if (GeomUtil.GetIntersectionPoint(M,
new Vector3(maxX + 0.1f, M.y, M.z), outer,
ref intersectionPoint, ref index0, ref index1))
{
// Intersection found
// Get the rightmost vertex of the intersecting line segment
int pindex;
Vector3[] triangle = new Vector3[3];
if (outer[index0].x > outer[index1].x)
{
pindex = index0;
// The triangle will be reversed depending on the vertex of the selected line segment, so adjust it so that it is clockwise.
triangle[0] = M;
triangle[1] = outer[pindex];
triangle[2] = intersectionPoint;
}
else
{
pindex = index1;
triangle[0] = M;
triangle[1] = intersectionPoint;
triangle[2] = outer[pindex];
}
If the intersection I and the vertex with the largest X coordinate of the line segment are the same, there is nothing to block from the vertex M, so it is not checked whether the triangle contains other vertices. If they are not the same, it is checked whether other vertices are included, but since the vertices included in the triangle are recessed vertices, the inclusion judgment is performed while satisfying that condition. If the triangle contains multiple vertices, the vertex with the smallest angle between the line segments M and I and the line segment M and the corresponding vertex is selected and stored in the finalIndex.
Middle 2 of CombinePolygon function
Vector3 P = outer[pindex];
int finalIndex = pindex;
// If the intersection and P are the same, there is nothing to block, so do not check the triangle
if((Vector3.Distance(intersectionPoint, P) > float.Epsilon))
{
float angleMin = 361f;
for(int i = 0; i < outer.Length; i++)
{
// Convex vertex / Reflective vertex check
int prevIndex = (i == 0)? outer.Length --1: i --1; // Previous vertex
int nextIndex = (i + 1)% outer.Length; // Next vertex
int nowIndex = i;
if (nowIndex == pindex) continue;
Vector3 outerP = outer[nowIndex];
if (outerP.x < M.x) continue;
// Ignore if the coordinates are the same duplicated at the time of division
if (Vector3.Distance(outerP, P) <= float.Epsilon) continue;
Vector3 prevVertex = outer[prevIndex];
Vector3 nextVertex = outer[nextIndex];
Vector3 nowVertex = outer[nowIndex];
// Is it a reflection vertex?
bool isReflex =! GeomUtil.IsAngleLessPI (nowVertex,
prevVertex,
nextVertex);
// Does the triangle contain "reflection vertices"?
if ((GeomUtil.IsInTriangle(outerP,
triangle[0],
triangle[1],
triangle[2]) <= 0)&&(isReflex))
{
// Invisible because the vertices are included in the triangle
// Find the angle between the M, I and M, outerP line segments (select the vertex with the shallowest angle)
float angle = Vector3.Angle(intersectionPoint - M, outerP - M);
if (angle < angleMin)
{
angleMin = angle;
finalIndex = nowIndex;
}
}
}
}
After finding the vertices (finalIndex) to join, join the vertex arrays of the inner and outer polygons.
Second half of Combine Polygon
Vector3 FinalP = outer[finalIndex];
// Join (create a new polygon)
List<Vector3> newOuterVertices = new List<Vector3>();
// Add up to Index that divides outer
for (int i = 0; i <= finalIndex; i++)
{
newOuterVertices.Add(outer[i]);
}
// Add all inner
for (int i = xmaxIndex; i < inner.vertices.Length; i++)
{
newOuterVertices.Add(inner.vertices[i]);
}
for (int i = 0; i < xmaxIndex; i++)
{
newOuterVertices.Add(inner.vertices[i]);
}
// Increase two vertices to split
newOuterVertices.Add(M);
newOuterVertices.Add(FinalP);
// Add the index of the remaining outer
for (int i = finalIndex + 1; i < outer.Length; i++)
{
newOuterVertices.Add(outer[i]);
}
outer = newOuterVertices.ToArray();
When the inner and outer polygons become one polygon, it is finally divided into triangles. First, initialize the index array of vertices and create an ear list.
InitializeVertices function
/// <summary>
/// Initialization
/// </summary>
void InitializeVertices(Vector3[] points)
{
vertices.Clear();
indices.Clear();
earTipList.Clear();
// Create index array
resultTriangulationOffset = resultVertices.Count;
for (int i = 0; i < points.Length; i++)
{
Vector3 nowVertex = points[i];
vertices.Add(nowVertex);
indices.AddLast(i);
resultVertices.Add(nowVertex);
}
// Search for convex triangles and ears
LinkedListNode<int> node = indices.First;
while (node != null)
{
CheckVertex(node);
node = node.Next;
}
}
The CheckVertex function that determines if a vertex is an ear looks like this:
CheckVertex function
void CheckVertex(LinkedListNode<int> node)
{
// Convex vertex / Reflective vertex check
int prevIndex = (node.Previous == null) ?
indices.Last.Value :
node.Previous.Value; // Previous vertex
int nextIndex = (node.Next == null) ?
indices.First.Value :
node.Next.Value; // Next vertex
int nowIndex = node.Value;
Vector3 prevVertex = vertices[prevIndex];
Vector3 nextVertex = vertices[nextIndex];
Vector3 nowVertex = vertices[nowIndex];
bool isEar = false;
// Is the internal angle within 180 degrees?
if (GeomUtil.IsAngleLessPI(nowVertex, prevVertex, nextVertex))
{
// Ear check
// Within 180 degrees, the triangle does not contain other vertices
isEar = true;
foreach(int i in indices)
{
if ((i == prevIndex) || (i == nowIndex) || (i == nextIndex))
continue;
Vector3 p = vertices[i];
// Ignore if the coordinates are the same duplicated at the time of division
if (Vector3.Distance(p, prevVertex) <= float.Epsilon) continue;
if (Vector3.Distance(p, nowVertex) <= float.Epsilon) continue;
if (Vector3.Distance(p, nextVertex) <= float.Epsilon) continue;
if(GeomUtil.IsInTriangle(p,
prevVertex,
nowVertex,
nextVertex) <= 0)
{
isEar = false;
break;
}
}
if (isEar)
{
if (!earTipList.Contains(nowIndex))
{
// Add ears
earTipList.Add(nowIndex);
}
}
else
{
// Exclude if it is no longer an ear when it is already an ear
if (earTipList.Contains(nowIndex))
{
// Ear removal
earTipList.Remove(nowIndex);
}
}
}
}
The actual triangulation is done in the following EarClipping function. As mentioned above, the vertices are taken out from the top of the ear list and the triangle connected to the front and back vertices is output. Then, the procedure of deleting the vertices of the ear from the vertex index array and determining whether the vertices before and after are the ears is repeated.
EarClipping function
void EarClipping()
{
int triangleIndex = 0;
while (earTipList.Count > 0)
{
int nowIndex = earTipList [0]; // Extract top
LinkedListNode<int> indexNode = indices.Find(nowIndex);
if (indexNode != null)
{
int prevIndex = (indexNode.Previous == null) ?
indices.Last.Value :
indexNode.Previous.Value; // Previous vertex
int nextIndex = (indexNode.Next == null) ?
indices.First.Value :
indexNode.Next.Value; // Next vertex
Vector3 prevVertex = vertices[prevIndex];
Vector3 nextVertex = vertices[nextIndex];
Vector3 nowVertex = vertices[nowIndex];
// Triangle creation
triangles.Add(new Triangle(
prevVertex,
nowVertex,
nextVertex, "(" + triangleIndex + ")"));
resultTriangulation.Add(resultTriangulationOffset + prevIndex);
resultTriangulation.Add(resultTriangulationOffset + nowIndex);
resultTriangulation.Add(resultTriangulationOffset + nextIndex);
triangleIndex++;
if (indices.Count == 3)
{
// End because it is the last triangle
break;
}
// Delete ear vertices
earTipList.RemoveAt (0); // Remove top
indices.Remove(nowIndex);
// Check the vertices before and after
int[] bothlist = { prevIndex, nextIndex };
for (int i = 0; i < bothlist.Length; i++)
{
LinkedListNode<int> node = indices.Find(bothlist[i]);
CheckVertex(node);
}
}
else
{
Debug.LogError("index now found");
break;
}
}
// UV calculation
for (int i = 0; i < vertices.Count; i++)
{
Vector2 uv2 = CalcUV(vertices[i], uvRect);
resultUVs.Add(uv2);
}
}
Make the result of triangle division into Mesh. In the EarClipping function, we prepare the necessary vertex array and index array (resultVertices and resultTriangulation) and pour them into Mesh.
MakeMesh function
void MakeMesh()
{
mesh = new Mesh();
mesh.vertices = resultVertices.ToArray();
mesh.SetIndices(resultTriangulation.ToArray(),
MeshTopology.Triangles, 0);
mesh.RecalculateNormals();
mesh.SetUVs(0, resultUVs);
mesh.RecalculateBounds();
MeshFilter filter = GetComponent<MeshFilter>();
if(filter != null)
{
filter.mesh = mesh;
}
}
By the way, I also set the UV coordinates. UV coordinates are assigned within the rectangular area of the polygon.
CalcUV
Vector2 CalcUV(Vector3 vertex, Rect uvRect)
{
float u = (vertex.x - uvRect.x) / uvRect.width;
float v = (vertex.y - uvRect.y) / uvRect.height;
return new Vector2(u, v);
}
I have explained the polygonal triangle division by the ear cutting method. It is important to use it, but if you draw a figure with the mouse, it will become a mesh in real time, you can make the outline data of the font a mesh, etc., but since it is not such a fast algorithm, if the number of vertices increases, it will be speedy. There will be problems (calculated in order by the CPU), but I find it interesting that complex polygons can be divided into triangles with a simple algorithm.
https://www.geometrictools.com/Documentation/TriangulationByEarClipping.pdf